Dopo aver ripreso a grandi linee quella che potremmo chiamare la genesi della crittografia, in questo secondo articolo ci porteremo molto in avanti nel tempo, fino ad arrivare ai giorni d'oggi.

Con l’avvento dei moderni calcolatori elettronici si è potuta sfruttare la potenza computazionale dei processori al fine di automatizzare le procedure di codifica e decodifica dei messaggi.

Concettualmente, nonostante siano passati secoli, si ragiona sempre nei termini di algoritmo, che rappresenta il metodo crittografico, e di chiave, una stringa scelta dall’utente utile a cifrare e decifrare il messaggio.

Una sostanziale differenza rispetto al passato è data dal fatto che gli elaboratori elettronici utilizzano quali input soltanto numeri binari, ovvero i numeri 0 e 1, con la combinazione dei quali vengono composti tutti gli altri numeri, lettere e simboli. In particolare per la formazione dell’alfabeto viene utilizzato un metodo di conversione denominato ASCII che permette di rappresentare fino a 128 caratteri alfabetici e simbolici tramite la combinazione di 7 cifre binarie.

L’introduzione degli algoritmi di cifratura a blocchi, inoltre, ha permesso di velocizzare i processi di cifratura/decifratura permettendo di applicare l’algoritmo non più a singoli elementi, ma ad interi blocchi di elementi (composti da N bit), sui quali è possibile effettuare diverse tipologie di operazioni, chiamate iterazioni o round le quali, eseguite in sequenza su ogni blocco elaborato, porteranno ad una maggiore o minore complessità dell’algoritmo di cifratura.

A partire dagli anni ‘70, unitamente alla diffusione dei personal computer, c’è stata una grande attenzione allo sviluppo di nuovi metodi di cifratura, che garantissero il migliore compromesso tra livello di sicurezza raggiunto e complessità in termini computazionali dell’algoritmo adottato. Il primo di questi fu creato dal tedesco Horst Feistel (crittografo tedesco naturalizzato statunitense che ha lavorato in IBM allo sviluppo di diversi famosi cifrari) il quale, con la sua cifratura Lucifer, pose le basi per il Data Encryption Standard (detto DES) primo protocollo di cifratura ufficialmente adottata dal National Bureau of Standard degli Stati Uniti (National Institute of Standards and Technology, un'agenzia del governo degli Stati Uniti d'America che si occupa della gestione delle tecnologie, oggi NIST) al fine di cifrare i documenti contenenti informazioni sensibili (in questo documento del NIST disponibile una breve spiegazione del DES).

Dopo alcuni anni, nonostante i miglioramenti apportati nel tempo, il protocollo DES fu soppiantato dal più performante e sicuro Advanced Encryption Standard (=AES) che, con i suoi blocchi da 128 bit, poteva utilizzare chiavi da 128, 192 o 256 bit e che, pertanto, è stato adottato dal NIST per cifrare documenti classificati perfino come Top Secret (a questa pagina del NIST un'ottima presentazione dell'algoritmo AES).

Crittografia simmetrica e crittografia a chiave pubblica

Dopo questi brevissimi richiami, che spero ci abbiano permesso di comprendere come e perchè si sia passati da un metodo di crittografia analogico a quello digitale, sarebbe opportuno focalizzare la nostra attenzione sul funzionamento di alcuni di essi.

Tra i metodi di crittografia attualmente più utilizzati in ambito informatico si potrebbe operare, semplificando parecchio, una sostanziale distinzione in base al tipo di chiave utilizzata: la crittografia a chiave simmetrica e la crittografia a chiave pubblica.

Nel primo caso, la chiave per cifrare e quella per decifrare sarà coincidente, nel secondo caso, invece, sarà necessario utilizzare due chiavi differenti (anche se “collegate” tra loro).

Una delle problematiche maggiori dei primi metodi di crittografia, come ad esempio il DES o l’AES, appena citati, consisteva nella necessità di creare una chiave piuttosto lunga, tanto da essere ragionevolmente sicuri che le capacità computazionali degli elaboratori non potessero eseguire un attacco definito brute force, ovvero un metodo che consiste nel provare tutte le possibili combinazioni di chiavi. Se è vero che è possibile minimizzare tale rischio semplicemente aumentando la lunghezza della chiave di cifratura, così da incrementare esponenzialmente i tempi di calcolo e rendere un attacco a forza bruta molto difficile (se non impossibile anche con gli apparati hardware attuali), bisogna però considerare che la principale pecca del metodo a chiave simmetrica era l’estrema difficoltà nel comunicare la chiave al destinatario in modo sicuro.

Questo delicato passaggio ha rappresentato per decenni il tallone d’Achille dei metodi di cifratura di questo tipo, spingendo alcuni studiosi a cercarne uno che permettesse al mittente ed al destinatario del messaggio di comunicare in totale sicurezza.

In effetti nella crittografia c’era un pezzo di storia ancora tutto da scrivere. Nel momento in cui fosse stato risolto tale dilemma sarebbe avvenuta una profonda rivoluzione, nella crittografia in particolare, ma anche più in generale nei metodi di comunicazione ritenuti fino ad allora sicuri.

Questa scoperta epocale avvenne negli anni ’70 in America, sviluppando l’intuizione avuta dai matematici Hellman, Diffie e Merkle secondo i quali ci si poteva scambiare in chiaro i valori utili a generare le proprie chiavi di cifratura, grazie all’utilizzo di funzioni dette unidirezionali, ovvero tramite funzioni non reversibili.

Poco dopo, grazie all’applicazione di altri studiosi ed appassionati di crittografia quali Rivest, Shamir ed Adleman fu messo a punto il sistema di crittografia considerato da allora tra i più importanti ed innovativi di questa branca della scienza: il sistema RSA (qui il paper), conosciuto anche come il sistema di crittografia a chiave pubblica.

L’idea innovativa consisteva nella presenza di due chiavi differenti, una pubblica, usata per cifrare il messaggio, l’altra privata, usata per decifrarlo. Ciò fu reso possibile grazie all’utilizzo di una funzione unidirezionale speciale, ovvero una funzione che fosse normalmente molto difficile da invertire tranne in determinate condizioni (=l’utilizzo della chiave privata).

In pratica, per utilizzare tale cifratura, ogni utente dovrebbe possedere due chiavi, provvedendo a creare prima di tutto una chiave privata, da conservare gelosamente, derivando poi dalla stessa una chiave pubblica. Tale chiave, come spiegato dal nome stesso, non è segreta, anzi, al fine di una corretta cifratura è necessario comunicarla al mittente del messaggio, il quale la utilizzerà per cifrare il proprio messaggio inviandolo così al destinatario senza la preoccupazione di dover comunicare anche la chiave, con i rischi che ne deriverebbero. Una volta che il messaggio è stato recapitato, ad esempio tramite email, il destinatario non deve fare altro che decifrare il messaggio tramite la propria chiave privata, l’unica in grado di invertire la funzione unidirezionale speciale che è alla base di questo metodo.

L’esempio classico riportato in letteratura scientifica vuole che Alice e Bob siano intenzionati a scambiarsi un messaggio di testo. Alice chiede a Bob la sua chiave pubblica, il quale provvede ad inviargliela. Tramite la chiave pubblica di Bob, Alice può cifrare il messaggio e può procedere ad inviarlo. Bob, una volta ricevuto il messaggio, lo può decifrare mediante la sua chiave privata.

Nella realtà la funzione utilizzata per implementare tale metodo è definita unidirezionale, ma ciò non significa che sia del tutto irreversibile poiché, tramite la fattorizzazione è possibile provare a risalire ai numeri primi usati per l’implementazione di tale sistema crittografico, anche se estremamente dispendioso in termini di potenza computazionale. Per ovviare a questo tipo di problema, oggi si consiglia l’utilizzo di chiavi che siano lunghe almeno 2048 bit.

A questa pagina troverete una spiegazione di tale algoritmo, anche con qualche piccola illustrazione che può facilitare la comprensione :-)

Per gli appassionati di numeri e problemi matematici, consiglio la lettura del libro L'ultimo teorema di Fermat. L'avventura di un genio, di un problema matematico e dell'uomo che lo ha risolto (ho inserito il link su Amazon per semplicità, ma lo trovate ovunque, anche in qualsiasi libreria tradizionale) anche stavolta di Simon Singh, il quale è riuscito a rendere appassionante un argomento di per sè ostico, ed inoltre è riuscito nell'immane intento di farmi leggere una enorme mole di cifre senza che me ne potessi annoiare!

Funzioni di Hash

Riprendendo il concetto di funzione non invertibile sopra descritta, sarà più agevole a questo punto introdurre il concetto di hash, poiché si basa su una funzione unidirezionale, semplice da calcolare ma (si spera) impossibile da invertire.

Il fine di tale algoritmo è ridurre un testo (o input) di lunghezza arbitraria in una stringa (detto valore di hash o message digest) di lunghezza prefissata.

Per di più, oltre alla non reversibilità, quindi all'impossibilità di risalire al messaggio iniziale partendo dal valore di hash, tale funzione deve rispettare altre caratteristiche importanti:

• deve produrre una stringa che abbia sempre la stessa lunghezza indipendentemente dalla misura dell’input;
• deve permettere che, qualora si ripeta la funzione di hashing su uno stesso messaggio, venga calcolato sempre lo stesso valore di output;
• infine deve garantire che alla minima variazione dell’input l’algoritmo restituisca un valore di hash completamente differente.

I protocolli di hashing più utilizzati sono: l’algoritmo MD5, uno dei primi algoritmi utilizzati a questo scopo, molto veloce e tuttora utilizzato per il controllo di integrità dei files; la famiglia di algoritmi SHA, offre un fattore di sicurezza crescente, i più conosciuti sono lo SHA-1 e lo SHA-256; la serie di algoritmi RIPEMD, il più conosciuto dei quali è il RIPEMD-160, nati come risposta europea all’algoritmo americano MD5.

A questo indirizzo ci potremo divertire a calcolare il valore di hash per qualsiasi porzione di testo e per files fino a 10 MB, mediante numerosi algoritmi di hashing

Le applicazioni di una simile funzione sono molteplici e più diffuse di quanto si possa immaginare. Un primo esempio di impiego delle funzioni di hashing sono i database delle password, dove le stesse vengono salvate sotto forma di valori di hash al fine di impedire a malintenzionati che ne venissero in possesso di risalire alle reali password.
Un altro esempio potrebbe essere la verifica di integrità dei file, per cui si utilizza il valore di hash come codice di controllo per essere certi che un determinato file non abbia subito modifiche.

È possibile verificare l’integrità di un messaggio, confrontandone il valore di hash calcolato prima e dopo la trasmissione del messaggio e verificando che nessuno abbia alterato il codice sorgente poiché, per le proprietà di tale funzione, una minima variazione dell’input provocherebbe una completa variazione del valore di hash. Un’utile applicazione di tale funzionalità è il confronto con liste di hash precompilate, al fine di poter rapidamente cercare file già censiti come virus o contenenti malwarein genere.

Anche in informatica forense la funzione di hash è molto utilizzata, al fine di preservare da qualsiasi tipo di alterazione o manipolazione i dati che vengono acquisiti, permettendone in ogni momento un rapido controllo di integrità. Tutti i dati che vengono duplicati per attività forensi, infatti, assumono validità solo se viene verificata la loro congruenza con il dato originale.

Per coloro che non abbiano mai sentito parlare di informatica forense, riporto una definizione molto esaustiva:

“L’informatica forense è la disciplina che studia la ricerca, identificazione, raccolta, preservazione, acquisizione, analisi, presentazione e valutazione dei dati informatici a fini probatori, nell’ambito del diritto processuale penale o civile. La scienza dell’informatica forense si snoda in diversi settori della tecnologia al fine di permettere al perito informatico di acquisire e analizzare diverse tipologie di dispositivi e di dati.”.

Fonte: https://www.dalchecco.it/formazione/terminologia/informatica-forense/

Qualsiasi elemento digitale è utilizzabile quale valore di input per una funzione di hash. Una stringa di testo, un’immagine, un file audio, interi hard disk o qualsiasi altro dato digitale potranno “passare” attraverso una determinata funzione di hash, restituendo un digest che avrà sempre la stessa lunghezza, in base all’algoritmo utilizzato.

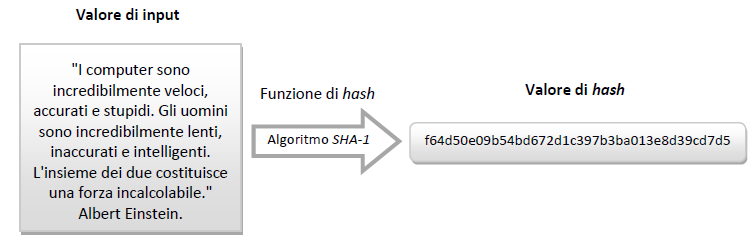
Qualche breve esempio potrà senz’altro offrire una vista d’insieme del concetto sopra esposto, rendendo immediatamente individuabili le caratteristiche e l’utilità delle funzioni di hash. In particolare, per tali esempi, è stato utilizzato l’algoritmo SHA-1:

Si noti come, al variare di un singolo carattere nel valore di input tra i due esempi sopra riportati (sostituendo il segno d’interpunzione finale dell’esempio in Fig. 1 con un punto esclamativo del valore di input in Fig. 2), il risultato ottenuto è stato completamente differente.

Allo stesso modo sarà agevole osservare che, utilizzando quale input un testo molto più lungo, la funzione di hash restituisca un valore sempre della stessa lunghezza (l’algoritmo SHA-1, preso ad esempio, genera un message digest di lunghezza pari a 160bit, rappresentato con 40 caratteri in valore esadecimale):

Nel protocollo Bitcoin, ad esempio, è stato utilizzato un particolare algoritmo di hash, detto hashcash, al fine di generare e validare i blocchi contenenti le transazioni e le relative intestazioni.

Firma digitale

Un’ulteriore applicazione della crittografia a chiave pubblica, unita alle caratteristiche dell’algoritmo di hash, è stata l’introduzione della cosiddetta firma digitale.

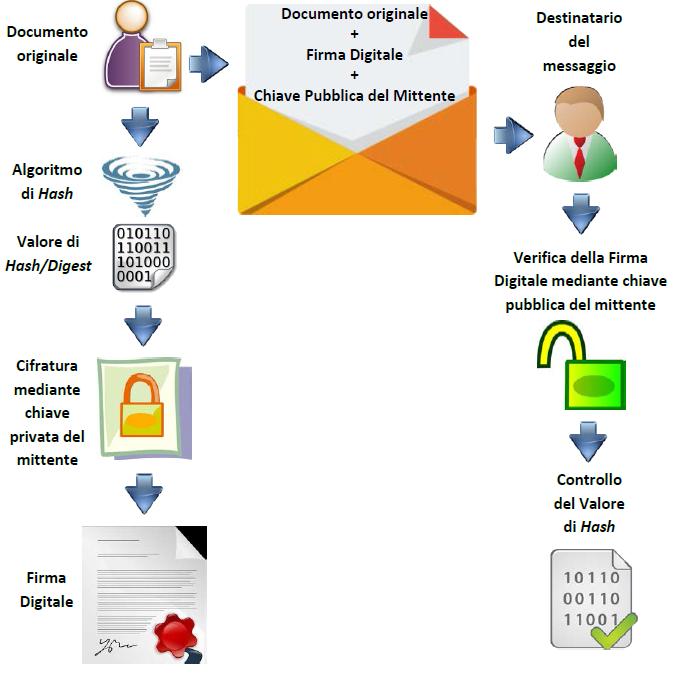
Si è già visto che, dato un documento con un contenuto a lunghezza arbitraria, sia possibile ridurlo ad una stringa mediante la funzione di hash. Tale stringa può essere crittografata con la chiave privata del mittente, invertendo il consueto ordine. Il documento, a questo punto, è pronto per essere inviato in chiaro al destinatario, unitamente alla firma digitale ed alla chiave pubblica del mittente. Il ricevente, a sua volta, utilizzando la chiave pubblica ricevuta dal mittente, potrà essere certo che il messaggio sia autentico e inoltre, calcolandone il valore di hash, che nessuno abbia potuto apportare variazioni al messaggio originale.

Lo schema successivo sarà utile al fine di comprendere meglio quali siano i passaggi necessari ad applicare la Firma Digitale ad un documento:

Negli ultimi anni la firma digitale è stata molto utilizzata oltre che ulteriormente implementata, anche mediante l’utilizzo di smart card, così da assumere un ruolo centrale nelle comunicazioni digitali, soprattutto nella Pubblica Amministrazione. Con il D.Lgs. 82/2005, seguito dal D.Lgs. 235/2010, è stato introdotto nella legislazione italiana il Codice per l’Amministrazione Digitale, un corpus di norme con cui è stata conferita la massima importanza alle comunicazioni digitali nella Pubblica Amministrazione, elevando la firma digitale ad una firma del tutto assimilabile a quella autografa (come indicato nell'art. 21, co.2, del Decreto Legislativo 7 marzo 2005, n. 82, pubblicato nella Gazzetta Ufficiale n. 112 del 16 maggio 2005) .

Anche nel protocollo Bitcoin gli sviluppatori si sono serviti della firma digitale, unitamente alla funzione di hash, per firmare digitalmente le transazioni e verificare che le stesse siano originate dal reale mittente, ma di questo ne parleremo nella terza ed ultima parte.